LE EQUAZIONI DI WOODWARD
La prima equazione chiarifica come la densità di un corpo cambi nel corso del tempo. Questa variazione dipende dall'energia interna del corpo stesso.


In particolare, il secondo membro dell'equazione è composto da una
costante ( 1/4 πG ) che moltiplica una sottrazione.
Il primo termine di questa sottrazione, contrassegnato
per l'appunto dal numero 1, può assumere valori positivi o negativi,
poiché la densità e la velocità della luce sono positivi,
ma la derivata seconda dell'energia può avere un valore negativo.
Questo primo termine fu chiamato da Woodward "Impuls Term" (termine
dell'impulso), perché è questo il principale responsabile della
spinta ottenuta.
Il secondo termine, contrassegnato dal numero 2,
è un prodotto di quadrati ( dal momento che entrambi i membri della
moltiplicazione - la costante e la derivata prima dell'energia - sono entrambi
elevati alla seconda potenza ), quindi è un prodotto positivo che però
diventa negativo per la presenza del segno "meno" davanti.
Questo secondo termine, quantitativamente molto inferiore rispetto al primo,
è stato definito come "Exotic Mass Generator Term" (termine
generatore di massa esotica).

La seconda equazione è stata ottenuta integrando la prima e spiega come la variazione di massa del corpo dipenda dalla potenza.
Legenda: m 0 è la massa “a riposo” del corpo, P la potenza e V il volume.
Come nella prima equazione, il secondo membro è composto da una costante
che moltiplica una sottrazione.
Il primo termine - contrassegnato dal numero 1 - può assumere valori sia positivi che negativi a causa della derivata prima della potenza.
Il secondo termine - contrassegnato dal numero 2 - è sempre negativo, perché l'operatore meno cambia segno a tutto ciò che viene dopo ( il primo termine della moltiplicazione è un quadrato, il secondo termine è il quadrato di una potenza diviso per un volume che, per definizione, è positivo ). Esso è chiamato
"Generatore di Massa Esotica".
Si ipotizza che questo secondo termine - trascurabile per piccole potenze, ma che tende invece a salire piuttosto rapidamente all'aumentare di esse, per via del quadrato - potrebbe essere responsabile della creazione di wormholes (cioè di tunnel spaziali).
SUPPLEMENTO PER ESPERTI, APPASSIONATI DI MATEMATICA E FISICA
COME SI ARRIVA ALLE EQUAZIONI DI WOODWARD ?
Il punto di partenza è costituito da un'equazione di campo (dove F è il potenziale):
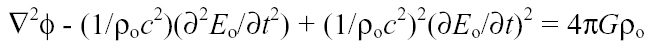
e dal Principio di Mach,
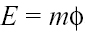
secondo cui il potenziale inerziale dei corpi non è altro che la risultante delle energie potenziali gravitazionali di tutta la materia dell'universo
Ma per la nota equazione di Einstein...
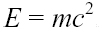
Da ciò deriva che...
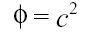
Usando la relazione tra energia, massa e energia potenziale si giunge all'espressione di un'equazione per il campo della forza di reazione inerziale.
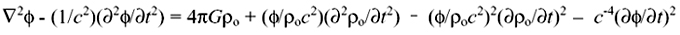
È stata così ottenuta una classica equazione d'onda, la D'Alembertiana
del potenziale di campo, che dipende dai valori di massa, densità ed energia locali.
Ne consegue che, se un corpo viene sottoposto da una forza esterna ad una
accelerazione, la sua energia interna cambi e di conseguenza anche la sua
densità e quindi la sua massa.
Il secondo membro dell'equazione è composto da quattro termini. Il
primo è una costante, il quarto è trascurabile per via della
presenza dell'inverso della quarta potenza della velocità della luce
nel vuoto. Il secondo e terzo termine sono i responsabili della variazione
di densità e quindi di massa.