INTRODUZIONE
L'astronomia moderna nasce con la comprensione che esistono leggi fisiche ben precise che regolano la vita, la morte e il moto di stelle e pianeti e di ogni altro corpo celeste.
Più ancora, nasce con la comprensione che queste leggi sono universali, cioè applicabili ad ogni angolo dell'Universo.
Per esprimere l'universalità di queste leggi fisiche è necessario utilizzare un linguaggio altrettanto universale, quello della matematica.
In questa sezione abbiamo voluto esporre alcune di queste leggi, comprensive delle relative formule.
LEGGI DI KEPLERO
Le Leggi di Keplero sono tre assiomi, di carattere geometrico, che descrivono il moto dei pianeti su un piano detto piano orbitale.
Sono state formulate dall'astronomo tedesco Johannes von Kepler all'inizio del XXVII secolo, sulla base dei dati ottenuti dalle osservazioni del collega Tycho Brahe.
Naturalmente, la formulazione originale delle Tre Leggi di Keplero si riferiva al Sole e ai pianeti del Sistema Solare: trattandosi di leggi universali, queste Leggi descrivono il moto di qualsiasi pianeta attorno a qualsiasi stella, sempre che vengano soddisfatti i loro limiti di validità.
Queste tre leggi, in ordine di formulazione, sono:
Prima Legge o LEGGE DELLE ORBITE ELLITTICHE (1609): l'orbita descritta da un pianeta è un'ellissi, in cui il Sole occupa uno dei due fuochi.
L'orbita ellittica di un pianeta prende il nome di eccentricità orbitale, che ha effetti sul suo ecosistema perché durante l'anno ci sarà un periodo in cui il pianeta è più vicino alla stella e uno in cui è più lontano, quindi un periodo in cui riceve più luce, calore e radiazioni e uno in cui ne riceve di meno.
Su pianeti privi di inclinazione assiale, o con una inclinazione minima, l'eccentricità orbitale crea stagioni con poche variazioni climatiche. Stagioni con differenza più marcate sono create dall'inclinazione assiale, perché una eccentricità eccessiva può pregiudicarne l'abitabilità, come nel caso di mondi di classe Q.
Su pianeti di classe M la differenza fra afelio (il punto in cui il pianeta è più lontano dalla propria stella) e perielio (il punto in cui è più vicino) è di solito limitata a valori molto bassi: nel caso della Terra parliamo di una eccentricità pari a 0.0167, ovvero meno del 2%.
L'esatta percentuale oltre la quale l'eccentricità orbitale diventa eccessiva dipende dall'estensione della Zona Abitabile, la quale a sua volta dipende dalla classe e dalla luminosità della stella.
La formula per calcolare l'eccentricità orbitale di un pianeta (e) è:
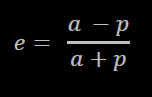
dove a = raggio dell'orbita all'afelio (ovvero l'asse maggiore dell'ellissi), e p = raggio dell'orbita al perielio (ovvero l'asse minore dell'ellissi), calcolati dal centro della stella al centro del pianeta.
La Flotta Stellare utilizza la Prima Legge di Keplero per avere una prima stima sull'abitabilità di un pianeta: dopo averne osservato una parte dell'orbita, è possibile calcolare i valori dei due semiassi dell'ellissi (a e p) e, da questi, calcolare l'eccentricità orbitale, che permette infine di verificare se l'intera orbita resta all'interno della Zona Abitabile oppure no.
Seconda Legge o LEGGE DELLE AREE (1609): il segmento che unisce il centro del Sole al centro del pianeta descrive aree uguali in tempi uguali.
Poiché, dalla Prima Legge, sappiamo che l'orbita è ellittica e non circolare e che, quindi, il pianeta può trovarsi più o meno vicino alla propria stella (eccentricità orbitale), la conseguenza della Seconda Legge di Keplero è che un pianeta si muove a velocità differenti: più veloce al perielio, più lentamente all'afelio.
Visto che, per restare all'interno della Zona Abitabile, l'eccentricità orbitale deve essere limitata (0.0167 nel caso della Terra), ne deriva che anche la differenza fra asse maggiore e asse minore deve essere limitata. Di conseguenza, le aree all'afelio e al perielio non saranno molto differenti, e così la velocità orbitale sarà abbastanza simile.
La formula per calcolare la velocità orbitale (v) di un pianeta in un dato punto dell'orbita è:

dove r = distanza istantanea dal centro della stella al centro del pianeta, e a = distanza massima tra il centro della stella e il centro del pianeta (afelio).
μ equivale al prodotto di G x M, dove G = Costante Gravitazionale Universale, e M = rapporto fra massa minore m1 (quella del pianeta) e massa maggiore m2 (quella della stella) = m1/m2.
Quando la differenza fra le due masse è notevole, come nel caso di una stella e di un pianeta di classe M, la massa minore può essere tralasciata, per cui M = m2, quindi μ = G x m2.
La Flotta Stellare utilizza la formula per il calcolo della velocità orbitale sia per determinare l'esatta posizione di un pianeta di cui sono noti i parametri (insieme ai dati sul moto proprio della stella, che indicano la sua velocità e la direzione del suo movimento), sia per adeguare la velocità di una nave stellare a quella del pianeta stesso, quando ci si accinga a raggiungerne l'orbita.
Terza Legge o LEGGE DEI PERIODI (1619): i quadrati dei tempi che i pianeti impiegano a percorrere le loro orbite sono proporzionali al cubo delle distanze medie.
La formula della Terza Legge è: 
dove T = tempo, d = distanza media tra il centro della stella e il centro del pianeta, e K una costante, detta "Costante di Keplero", che vale "1" per il caso di pianeti di classe M che ruotino attorno alla propria stella.
In questo caso, quindi, la formula della Terza Legge può essere semplificata in: 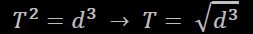
Conoscendo d, quindi, è facile calcolare la durata di un anno di qualsiasi pianeta, espresso in percentuali di anno terrestre.
Nel caso del pianeta Vulcano (40 Eri II), che ha una distanza media dalla sua stella pari a 0.56 UA (84 milioni di km), la formula risulta: 
L'anno solare di Vulcano, quindi, risulta pari a 365,25 x 0,419 = 153 giorni standard (si noti che questo numero non fornisce informazioni né sulla durata del giorno vulcaniano, né su quanti giorni vulcaniani ci siano in un anno di quel pianeta).

ZONA ABITABILE
La Zona Abitabile (o, più propriamente, la Zona Abitabile Circumstellare) è la regione di spazio, all'interno di un sistema stellare, in cui è più probabile trovare pianeti di classe M, ovvero pianeti abitabili in grado di supportare forme di vita umanoidi.
Il presupposto per avere un pianeta di classe M (o assimilabile, come i pianeti di classe O) è la presenza di acqua liquida sulla superficie.
Questa presenza, a sua volta, dipende direttamente da due fattori: l'energia emessa dalla stella e la distanza del pianeta dalla stella stessa.
Basandoci sull'unico esempio disponibile, il Sistema Solare della Terra, è stata sviluppata una formula, suddivisa in due parti: la prima determina la "distanza ottimale" per tale pianeta, la seconda determina l'ampiezza della fascia a partire da questa distanza ottimale.
La formula per calcolare la distanza ottimale è:
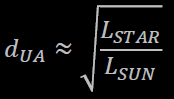
dove dUA è la distanza del pianeta dalla stella, espresso in unità astronomiche, LSTAR è la luminosità della stella e LSOL quella del Sole.
Poiché l'energia emessa da una stella diminuisce con il quadrato della distanza, la distanza ottimale per un pianeta abitabile di una stella con LSTAR = 2 LSOL sarà pari a √2 , ovvero a 1,41 UA.
Analogamente, per una stella con LSTAR = 1/2 LSOL la distanza ottimale di un pianeta abitabile sarà pari a √0,5 , ovvero a 0,71 UA.
Una volta ottenuta la distanza ottimale, è necessario calcolare l'ampiezza della Zona Abitabile.
Per ottenere questo risultato non esiste una formula matematica, ma una osservazione empirica basata - di nuovo - sui pianeti del Sistema Solare.
Venere (Sol II) si trova a 0,723 UA dal Sole, ed è considerato un pianeta al confine estremo della "Zona Calda". Si può quindi stimare che la Zona Abitabile del Sistema Solare incominci a 0,75 UA dal Sole.
Marte (Sol IV), all'estremo opposto, si trova a 1,524 UA dal Sole. Se non fosse geologicamente "morto" sarebbe all'estremo limite della Zona Abitabile, che si può quindi stimare si estenda almeno fino a 1,5 UA.
Pertanto, la Zona Abitabile di una stella dovrebbe essere compresa fra 0,75 e 1,5 volte la distanza ottimale.
Queste formule permettono di calcolare l'area circumstellare in cui è più probabile trovare acqua liquida, quindi pianeti di classe M e, di conseguenza, forme di vita umanoide.
È però bene ricordare che sono possibili pianeti abitati da forme di vita umanoide anche in altre regioni di un sistema stellare (è il caso, ad esempio, di Andoria o dei pianeti di classe R), e che esistono forme di vita, anche senzienti, che prosperano in ambienti incompatibili con la vita umanoide (è il caso di Tholia, Excalbia o degli oceani subglaciali di Europa, solo per citare alcuni esempi).
Di conseguenza, la ricerca di "nuove forme di vita e nuove civiltà" non può, e non deve, limitarsi alla Zona Abitabile di una stella.

LIMITE DI ROCHE
Il Limite di Roche è la distanza minima fra due corpi celesti, di massa differente e tenuti insieme solo dalla forza di gravità, superata la quale il minore dei due corpi si frammenta a causa delle forze di marea. Tipicamente, il Limite di Roche opera fra una stella e un pianeta o fra un pianeta e un satellite (anche artificiale).
La formula del Limite di Roche è:
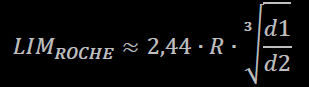
dove R = raggio del corpo maggiore, d1 = densità del corpo maggiore e d2 = densità del corpo minore.
Come si evince da d1/d2, nel caso di due corpi di densità simile questo valore si approssima ad 1, mentre se il primo corpo ha una densità minore rispetto al secondo (è il caso di, rispettivamente, una stella e un pianeta), il Limite di Roche è inferiore.
Nel caso del Sole (R = 700.000 km, d1 = 1.408) e della Terra (d2 = 5.514), la formula restituisce i seguenti valori:

che significano che un pianeta di classe M non può trovarsi a meno di circa 1.100.000 km da una stella di classe G, valore che corrisponde a 0.0072 Unità Astronomiche: una distanza così bassa che il pianeta sarebbe sostanzialmente fuso, quindi ben lontano da essere un mondo di classe M...

LIMITE DI CHANDRASEKHAR
Il Limite di Chandrasekhar indica il limite di massa non rotante che può opporsi al collasso gravitazionale di una nana bianca, sostenuto dalla pressione di degenerazione degli elettroni.
Durante la fasi finali della propria esistenza, una stella tende ad accumulare materia degenere nel proprio nucleo.
Quando le reazioni nucleari si arrestano, il destino della stella è determinato dalla sua massa residua: se è inferiore a 1.4 masse solari la stella diventa una nana bianca, se è superiore diventa una supernova.
Il Limite di Chandrasekhar rappresenta, quindi, il discrimine fra nana bianca e supernova al termine della vita di una stella della sequenza principale.
La formula che descrive il Limite di Chandrasekhar è:
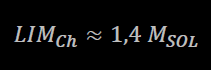
dove MSOL è la massa del Sole, pari a 1,989 x 1030 kg. La Massa di Chandrasekhar, quindi, corrisponde a ≈ 1,4 x 1,989 è ≈ 2,785 x 1030 kg

LIMITE TOV
Il Limite TOV (dalle iniziali dei tre scienziati che lo hanno calcolato: Tolman, Oppenheimer e Volkoff) è collegato al Limite di Chandrasekhar e descrive lo stadio evolutivo di una stella successivo alla supernova.
In base al Limite di Chandrasekhar, perché alla fine della propria vita una stella diventi una supernova deve avere una massa residua - al termine di ripetuti processi di espulsione di massa - pari o superiore a 1.4 masse solari.
Se ciò che resta di una supernova ha una massa compresa fra 1.4 e 3 masse solari, la stella si trasforma in una stella di neutroni.
Se ciò che resta di una supernova ha una massa che supera le 3 masse solari, la stella si trasforma in un buco nero.
La massa esatta che permette di discriminare fra stella di neutroni e buco nero non è precisamente calcolabile con una formula universale, perché dipende in parte dalla metallicità della stella originale e in parte da altri fattori che non sono ancora pienamente compresi.
